MYSTERIUM COSMOGRAPHICUM
HOW TO MAKE YOUR OWN PLATONIC SOLIDS
PAPER POLYHEDRA AND THE SECRET OF THE UNIVERSE
By Rebecca Elliott
INTRODUCTION: All shapes begin with the triangle.
All shapes begin with the triangle: it’s the simplest polygon that can be drawn: three points and three sides: see the father the son the holy spirit: see the pyramid: the cat’s ear: see the symbol of the Illuminati inscribed on the back of the US dollar bill. See above: house, sandwich, pizza, Bermuda Triangle.
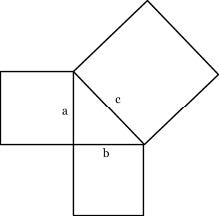
The Pythagorean Theorem:
a2 + b2 = all triangles are holy
For a better idea of what this means, imagine a triangle with its points sharp in your throat, liver, and spleen. This triangle is the seat of emotion; it buries itself in your organs and scrapes against the inside of your skin as it rotates.
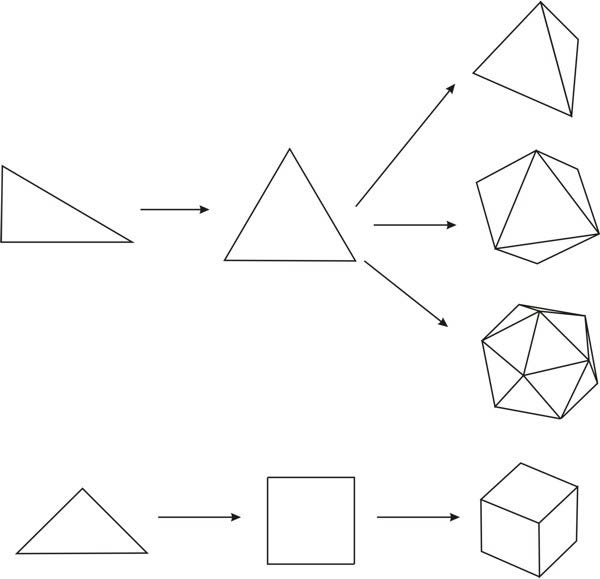
Plato’s Timaeus demonstrates that four of the regular polyhedra, commonly known now as the Platonic solids, can be formed from two types of triangles: the equilateral triangle and the right isosceles, or “half square.” (He ignores for the moment the fifth, the dodecahedron, which tends to turn up only to complicate things, representing spirit, the heavenly sphere, its twelve sides the twelve signs of the zodiac.)
On July 19, 1595, twenty-five year old Johannes Kepler was giving a lecture on the conjunction of Jupiter and Saturn. As he plotted out their course on the blackboard, he noticed that the conjunctions formed a series of triangles that transcribed a circle:
At that moment the triangles brought Kepler what he described as an epiphany. There were six known planets and five Platonic solids to fit between them: the relation of the planets’ orbits, existing in three dimensional space, must correspond to the three dimensional polyhedra. All shapes begin with the triangle.
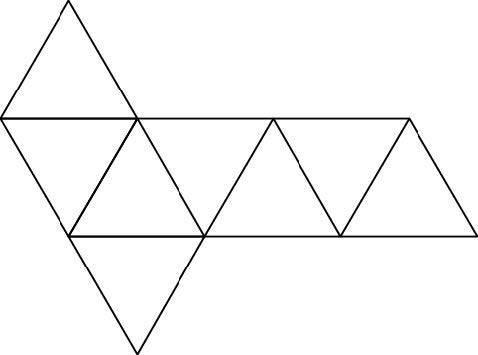
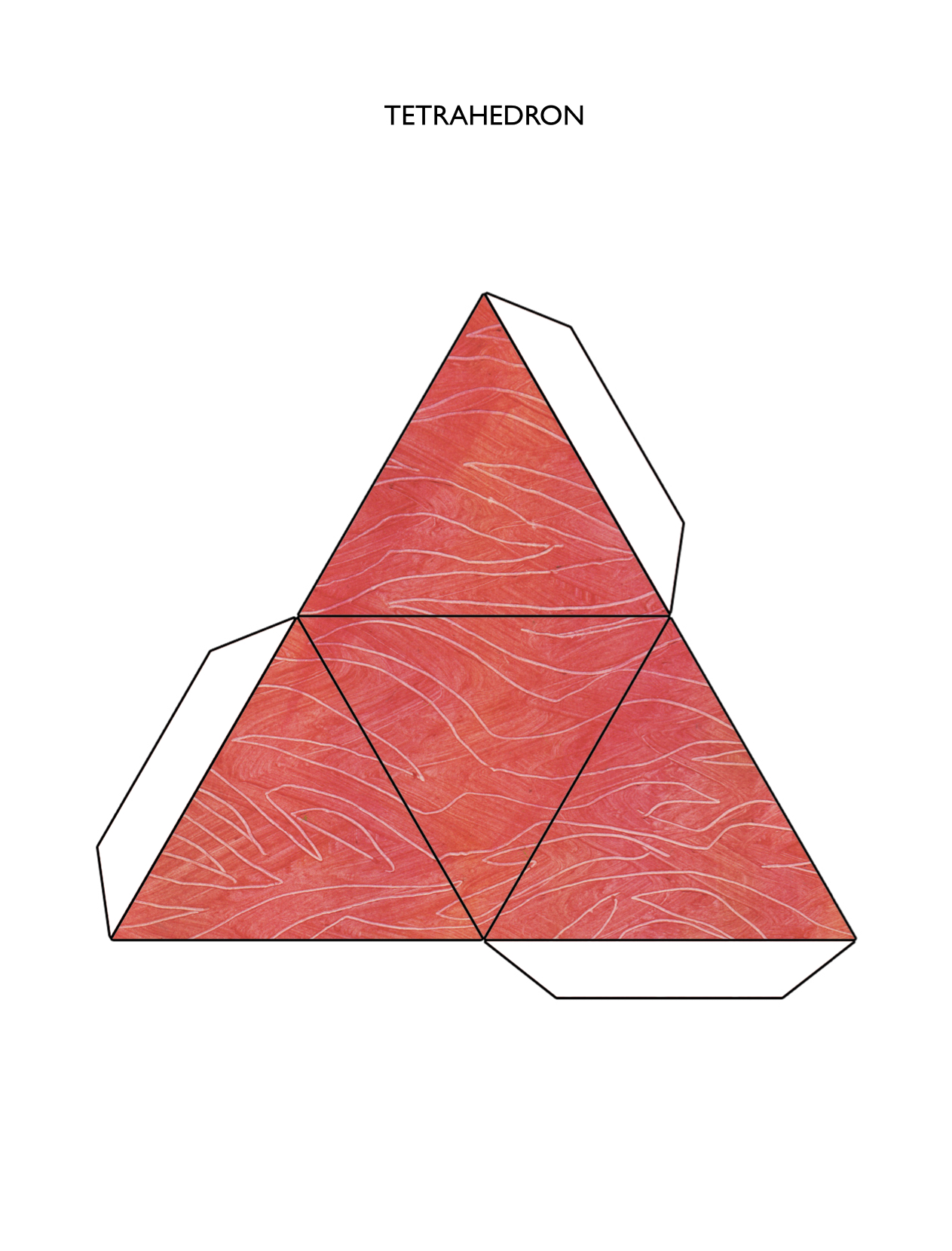
1: Tetrahedron
I’ve begun building paper models of polyhedra. The idea is to attach a piece of string to one of the points and hang them around my desk, then to stare at them while they spin in phantom breezes — you know, the breezes that can only be seen and not felt, in the winter when the windows are shut for three months and the air has nothing to do but to follow the heat of your body as you move around the cold apartment, lazy as a cat. As they turn, the polyhedra cast light and shade as one face after another catches the lamplight and sends it flying across the room, just briefly, before it revolves again into shadow.
For the Greeks, the four elements — fire, earth, air, and water — took the shape of tiny polyhedra. Fire, as the sharpest and the lightest, was composed of the simplest polyhedron: four equilateral triangles fold up into a three-dimensional shape with four sharp vertices.
This is why fire burns — because we’re always poking ourselves against its points.
For we shall concede to no one that there are visible bodies more perfect than these.
(Plato, Timaeus)
2: The Cube
Kepler inscribed the five Platonic solids in spheres and nested them one inside the other, and then put the six planets’ orbits along the spheres. A larger sphere, which held the fixed stars, went on the outside. Just inside of that was Saturn, and between the orbits of Saturn and Jupiter he fit the cube. The cube represented the element of Earth to the Greeks, and was considered by Kepler the most “dignified” polyhedron – all of its sides and edges being parallel and perpendicular, and representing the three dimensions of space. Although this theory turned out later to be completely wrong, he found a way to make each of the shapes fit between the orbits of the planets. This geometry of perfect order was proof of God’s plan for the universe, and was the explanation for the number of planets. There were six planets because there were five regular polyhedra to fit between them.
And how intense was my pleasure from this discovery can never be expressed in words. I no longer regretted the time wasted. Day and night I was consumed by the computing, to see whether this idea would agree with the Copernican orbits, or if my joy would be carried away by the wind. Within a few days everything worked, and I watched as one body after another fit precisely into its place among the planets.
(Kepler, Mysterium Cosmographicum)
At this point I want to make sure you’re still with me. Have you been following along? What I’d really like is if you would turn to the appendix at the end of this essay and use the printouts there to make paper polyhedron models along with me. Of all these shapes, the cube is the most familiar, and so the least interesting. Were you thinking of skipping it and moving on to constructing more intriguing paper models, like the icosahedron, or even the dodecahedron? I would very gently advise you against it. The cube’s ubiquity in our everyday life is exactly what makes it so important to study: because you see it everywhere, you’re in danger of not seeing it at all. I’ve had the cube hanging from a string next to my desk for a month now, and I’ve spent some time looking at it every day, but it wasn’t until a couple of days ago that I noticed its actual shape, and this realization led me to reevaluate the shape of everything else. The best thing you can do is hang the cube from one of its points – whatever you do, don’t set it flat on the table next to you. Hung like this, from an angle, the faces aren’t squares: they’re diamonds: or rhombuses: or skewed and glowing planes. The whole shape takes on another form altogether. If you still can’t see it, put the cube in front of a harsh light and trace the outline of the shadow it casts on the wall. What shape is it? It is the solid weight of your bones. It is no sharp thing. It is the shape of your foot on the bare, red earth.
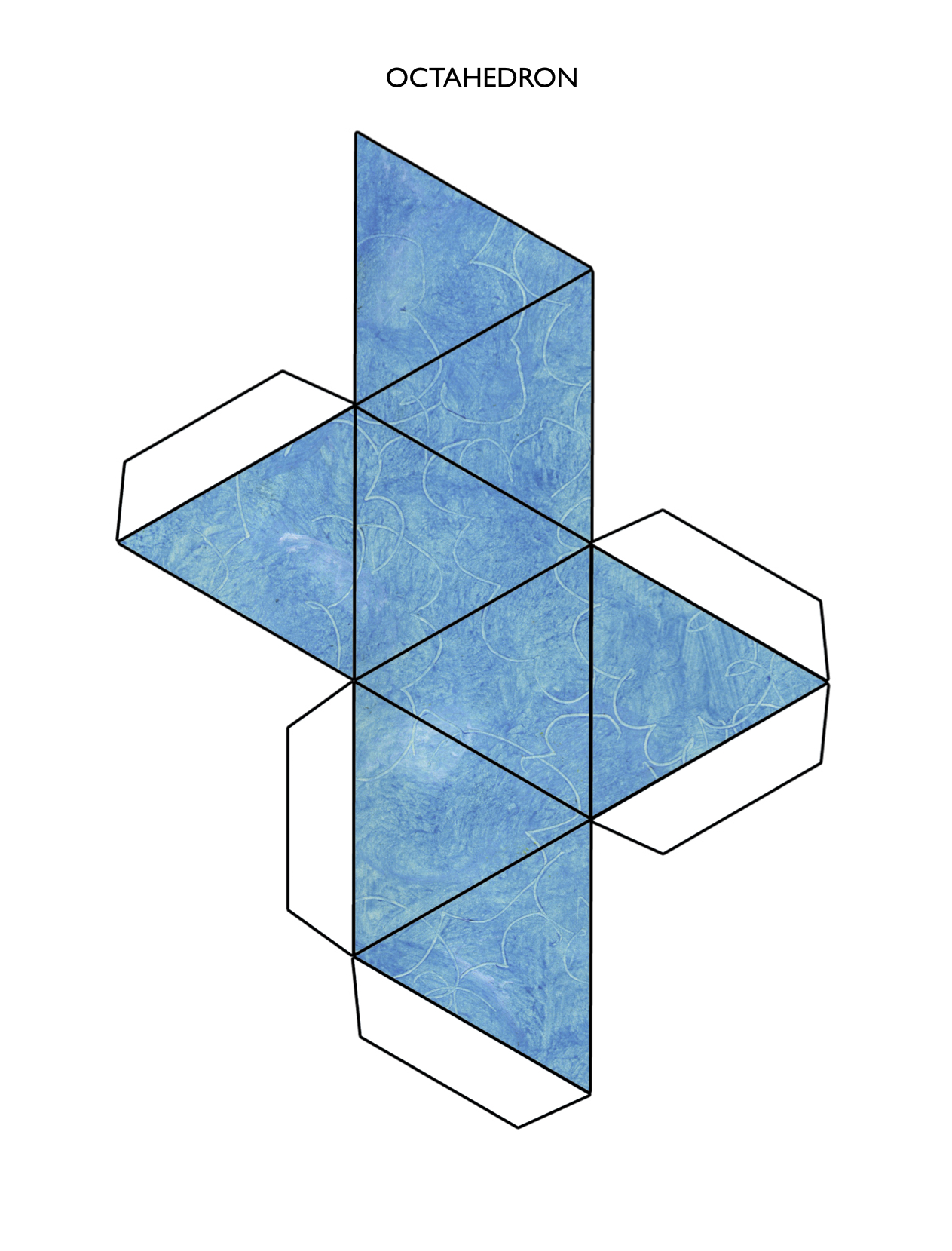
3: The Octahedron
What is it that makes us look for shapes and numbers in the stars?
What makes us find them?
4: The Icosahedron
Mathematics is the realm of perfection, and if the universe fits into our ideas of mathematical order, then we are less alone: everything isn’t terrible and random: perfection and order and god exist. The epiphany is the sound of all the planets clicking into their places among the heavenly shapes.
But there are not six planets nestled between five heavenly polyhedra, and the stars aren’t fixed and don’t circle us but occupy their own complicated geometries – so these shapes have fallen back to earth. Let’s pick them up and see what can be done with them now. Just because the sky wants nothing to do with them doesn’t mean they’re any less sacred.
For example, imagine you live in a city that couldn’t be any farther from the stars and planets. You ride on an endless train through white trees and satellite dishes lifting their blank faces toward an invisible sun. Time exists because the stars and planets move across the sky, and it is inseparable from them: in this place with no stars, there is also no time, and so you are riding the train forever, and the white trees exist in the same moment as the buildings, their bricks, and the sky which is solid white and doesn’t end but extends down into the buildings and each of their bricks and the train where you sit and hold in your lungs an icosahedron.
The icosahedron, as you know, is water, and makes it difficult to breathe.
Is this religion or magic or poetry?
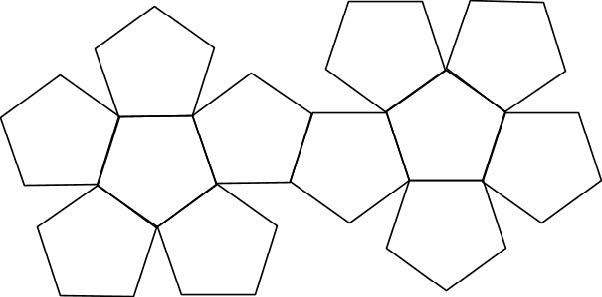
5: The Dodecahedron
(Plato, Timaeus)
On the other side of epiphany is the moment when you realize everything you believed was true is actually false. The light shifts: the colors change. What matters most is what you do next.
I imagine at this point you are standing in a forest. The trees here are straight and tall and close together, all pines with red-gray bark and branches that start far above you at the edge of your vision. The brown pine needles covering the forest floor muffle any sound, but there is no sound. You might start walking until you find a clearing and then begin to repopulate the black sky with stars, or you might place your hand against the nearest trunk and feel the rumbling of the beetles locked inside.
Appendix: Polyhedral Nets
A net is a two-dimensional arrangement of polygons that can be cut out and folded up into a three-dimensional polyhedron. Follow these instructions to make your own paper polyhedra, which can be used as decoration, dice, or a representation of the harmony of the universe.
- Print out these templates on a heavy cardstock.
- Cut out along the thick outline using scissors or a knife.
- Score the lines before folding – this is optional, but makes for cleaner folds and is especially important when using thick paper or cardboard. You can score the lines using the back of a butter knife, or make very light cuts with an xacto knife.
- Glue in the tabs.
Rebecca Elliott lives in Chicago, where she makes artist's books & letterpress prints with friends as Meekling Press. Her parents are scientists who filled the house with paper polyhedra when she was very young, and who would recommend checking out Magnus Wenninger's book Polyhedron Models, if you're into that kind of thing.
© 2015